(The R code for Barnard’s exact test is at the end of the article, and you could also just download it from here, or from github)
About Barnard’s exact test
About half a year ago, I was studying various statistical methods to employ on contingency tables. I came across a promising method for 2×2 contingency tables called “Barnard’s exact test“. Barnard’s test is a non-parametric alternative to Fisher’s exact test which can be more powerful (for 2×2 tables) but is also more time-consuming to compute (References can be found in the Wikipedia article on the subject).
The test was first published by George Alfred Barnard (1945) (link to the original paper in Nature). Mehta and Senchaudhuri (2003) explain why Barnard’s test can be more powerful than Fisher’s under certain conditions:
When comparing Fisher’s and Barnard’s exact tests, the loss of power due to the greater discreteness of the Fisher statistic is somewhat offset by the requirement that Barnard’s exact test must maximize over all possible p-values, by choice of the nuisance parameter, π. For 2 × 2 tables the loss of power due to the discreteness dominates over the loss of power due to the maximization, resulting in greater power for Barnard’s exact test. But as the number of rows and columns of the observed table increase, the maximizing factor will tend to dominate, and Fisher’s exact test will achieve greater power than Barnard’s.
About the R implementation of Barnard’s exact test
After finding about Barnard’s test I was sad to discover that (at the time) there had been no R implementation of it. But last week, I received a surprising e-mail with good news. The sender, Peter Calhoun, currently a graduate student at the University of Florida, had implemented the algorithm in R. Peter had found my posting on the R mailing list (from almost half a year ago) and was so kind as to share with me (and the rest of the R community) his R code for computing Barnard’s exact test. Here is some of what Peter wrote to me about his code:
On a side note, I believe there are more efficient codes than this one. For example, I’ve seen codes in Matlab that run faster and display nicer-looking graphs. However, this code will still provide accurate results and a plot that gives the p-value based on the nuisance parameter. I did not come up with the idea of this code, I simply translated Matlab code into R, occasionally using different methods to get the same result. The code was translated from:
Trujillo-Ortiz, A., R. Hernandez-Walls, A. Castro-Perez, L. Rodriguez-Cardozo. Probability Test. A MATLAB file. URL
http://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=6198
My goal was to make this test accessible to everyone. Although there are many ways to run this test through Matlab, I hadn’t seen any code to implement this test in R. I hope it is useful for you, and if you have any questions or ways to improve this code, please contact me at calhoun.peter@gmail.com
Using the R function for Barnard’s exact test
# source("https://www.r-statistics.com/wp-content/uploads/2010/02/Barnard.R.txt") # downloading the code from the website
# Loading the function
source("https://www.r-statistics.com/wp-content/uploads/2012/01/source_https.r.txt") # Making sure we can source code from github
source_https("https://raw.github.com/talgalili/R-code-snippets/master/Barnard.R")
# Using the function
#Examples:
Convictions <-matrix(c(2, 10, 15, 3), nrow = 2, dimnames = list(c("Dizygotic", "Monozygotic"), c("Convicted", "Not convicted")))
fisher.test(Convictions, alternative = "less")
Barnard(Convictions)
And here is the output
> #Examples:
> Convictions <-matrix(c(2, 10, 15, 3), nrow = 2, dimnames = list(c("Dizygotic", "Monozygotic"), c("Convicted", "Not convicted")))
> fisher.test(Convictions, alternative = "less")
Fisher's Exact Test for Count Data
data: Convictions
p-value = 0.0004652
alternative hypothesis: true odds ratio is less than 1
95 percent confidence interval:
0.0000000 0.2849601
sample estimates:
odds ratio
0.04693661
> Barnard(Convictions)
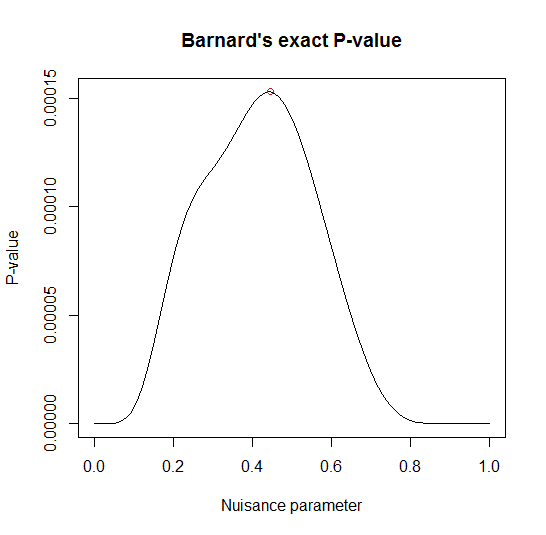
2x2 matrix Barnard's exact test: 100 13x19 tables were evaluated
-----------------------------------------------------------
Wald statistic = 3.6099
Nuisance parameter = 0.44446
p-values: 1-tailed = 0.00015285 2-tailed = 0.00030569
-----------------------------------------------------------
Final note: I would like to thank Peter Calhoun again for sharing his code with the rest of us - Thanks Peter!
Update (21.04.2010): In case you are facing a table with structural zeros (that is, missing values in the table), the package aylmer might be able to help you (it offers a generalization of Fisher's exact test)
Update (16.06.2011): A more updated (and faster) code is now available on the post (thanks goes, again, to Peter Calhoun). The post is updated with a newer example. The old R code for the function can still be found here.
Update (12.04.2012): I just found out that there is a new R package (from 2011-11-21) that also implements Barnard's test. You can find it here.